
Points de réapprovisionnement et stocks de sécurités optimaux en gestion d'inventaires
Rédigé par Vincent Béchard le 2020-01-14
La nécessité d'optimiser la gestion des inventaires
Je suis un expert en simulation. À mes yeux, un processus est un graphe orienté d’étapes de production. Entre les étapes, il y a des zones tampons. Ces tampons absorbent la variabilité et les problèmes de timing imparfait. Sans capacité tampon, aucun processus ne fonctionnerait de manière efficace et fluide. Qu'en est-il de l'inventaire ? Il s'agit simplement d'une capacité tampon plus volumineuse et à plus long terme.
Récemment, j'ai eu plusieurs mandats hors simulation où la compréhension des processus était essentielle, mais aucun modèle n'a été construit. Les objectifs étaient de définir les niveaux min-max appropriés pour la gestion des stocks. En travaillant sur ces problèmes, j'ai réalisé que nous considérons les inventaires comme un paramètre de conception à déterminer, et non comme un tampon résultant entre les étapes du processus. Par conséquent, nous nous concentrons sur la gestion du processus d'inventaire plutôt que sur les processus qui génèrent un besoin d'inventaire!
Les défis réels de la gestion des inventaires
La manière traditionnelle d'établir des seuils de stocks consiste à examiner les données récentes des taux de consommation (ou : demande, prévisions) et les délais de livraison des commandes. Il existe plusieurs formules pour calculer les min-max adéquats, les stocks de sécurité, les points de réapprovisionnement, etc. Cette technique est simple et utile si :
- La moyenne et la variance du délai de livraison et de la demande sont constantes dans le temps (distribution stable dans le temps)
- La distribution est approximativement Normale (symétrie, car des intervalles de tolérance sont impliqués dans les formules)
- Les délais ainsi que les demandes sont indépendants (les délais ou les demandes ne seraient pas indépendants si l'on trouvait souvent plusieurs valeurs basses successives et plusieurs valeurs hautes successives par exemple)
Par conséquent, nous supposons que les seuils min-max sont des valeurs constantes invariantes dans le temps. Que se passe-t-il si la demande moyenne évolue dans le temps (saisons, cycles, équipes), que se passe-t-il si les délais ne sont pas répartis symétriquement ? Les graphiques de la figure 1 illustrent des données typiques.
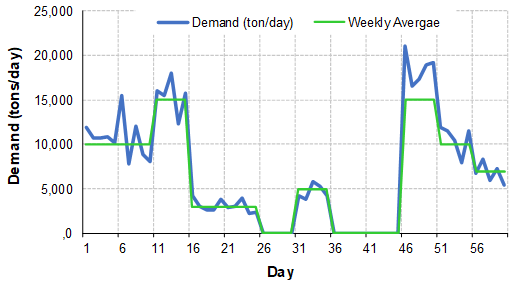
Figure 1a: Courbes de la demande et dex prévisions
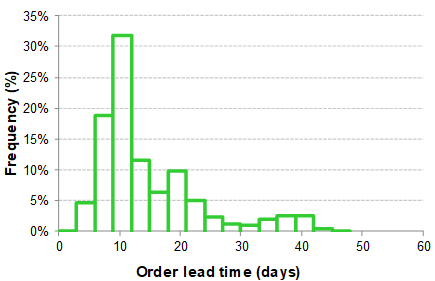
Figure 1b: Variabilité dans les délais de livraison
Réapprovisionnement basé sur simulation pour minimiser les stocks de sécurité
Pourquoi avons-nous inventé le concept min-max ? Pour avoir une règle simple pour minimiser les niveaux d'inventaires sans rupture de stock, et limiter les surstocks en suggérant quand arrêter de commander. Reformulons mathématiquement : le but est de minimiser les niveaux de stocks (pas d’argent dormant) sous la contrainte de ne jamais être vides. Notre technique est basée sur cette équation d'équilibre fondamentale basée sur le temps :
où It est le niveau d'inventaire à la fin de la période t, R est la quantité totale reçue pendant la période t et D est la demande (ou consommation) totale pendant la période t. Voici les grandes lignes de l'algorithme de réapprvisionnement optimal :
- Obtenir la demande prévue pour les prochaines périodes (horizon temporel fini), le niveau d'inventaire initial, les dates de réception prévues et les quantités des commandes en cours
- Calculer la demande et la réception cumulées prévues (total depuis le lancement jusqu'à l'instant t)
- Trouver la première période pendant laquelle la réception cumulée est toujours supérieure mais touche la courbe de demande cumulée
- Replanifier une commande en tenant compte d'un délai raisonnable pour la quantité manquante
- Répéter 3 à 4 pour toutes les périodes restantes
- Lister les points de réapprovisionnement (ou dates) et les quantités idéaux et tracer la tendance des stocks à l'aide de l'équation basée sur le temps
Avez-vous encore remarqué? L'inventaire est la conséquence de décisions concernant la réception et la demande… L'algorithme gère les points de réapprovisionnement pour s'assurer que le niveau d'inventaire sous-jacent est toujours positif. Si vous appliquez cet algorithme, vous obtiendrez quelque chose comme ceci :
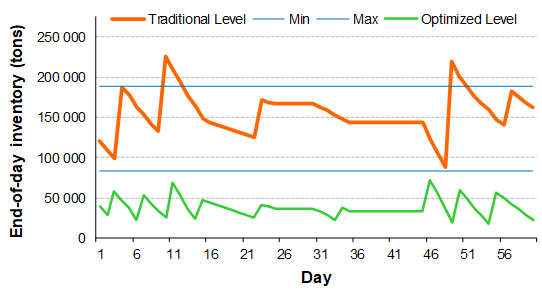
Figure 2a: Tendance du niveau d'inventaire
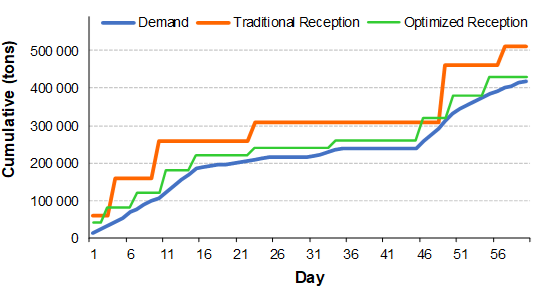
Figure 2b: Inventaire cumulé et points de réapprovisionnement
La courbe orange sur la figure 2a montre les limites min-max typiques. Si l'approche habituelle de gestion des inventaires était utilisée, nous commanderions de nouveaux produits uniquement lorsque la demande prévue entraînerait un stock inférieur au minimum. Le niveau d'inventaire varie généralement entre les niveaux minimum et maximum (courbe orange).
Les courbes vertes sur les figures 2a et 2b illustrent le résultat de l'algorithme de réapprovisionnement optimal présenté précédemment. La réception cumulée (en vert sur la figure 2b) est strictement au-dessus de la courbe de demande cumulée avec une marge. Cette marge agit comme un niveau minimum (ou stock de sécurité) qui prend en compte la variabilité des délais et la demande prévue variant dans le temps. C’est comme si la spécification de stock minimum s’adaptait à une demande variable dans le temps au lieu d’être constante. Si cette approche optimale était utilisée, les niveaux de stock indiqués par la courbe verte dans la figure 2a seraient bien inférieurs au niveau de stock que nous obtiendrions à partir de l'approche min-max "traditionnelle" (courbe orange).
Quelques améliorations pratiques
L'algorithme présenté ci-dessus est trop simpliste pour des applications réelles. Nous avons incorporé plusieurs améliorations. Mon préféré : la simulation Monte-Carlo pour estimer les risques de rupture de stock ou de dépassement de capacité de stock!
L'idée est d'induire une variabilité des délais selon leur répartition mais aussi dans la prévision de la demande (les volumes prévus sont souvent révisés dans le temps…). La simulation génère de nombreuses courbes de réception cumulées et agrège les résultats de telle sorte que 95 % ou 99 % des fois, la courbe de réception cumulée est supérieure à la courbe de demande cumulée.
Et puis, il est possible d'envisager des créneaux horaires : des commandes groupées si trop rapprochées dans le temps car le transporteur les regrouperait de toute façon. Et pourquoi pas : imposer un délai de sécurité pour garantir que tout le matériel requis arrivera juste avant le début de la production. Et bien d'autres ajustements de la même nature...
En conclusion
Les concepts de stocks de sécurité, de points de réapprovisionnement et de niveaux d'inventaire min-max (stocks de sécurité) sont pratiques, simples à utiliser, mais... peut-être pas adaptés à la vie réelle. Avec les systèmes intelligents programmables modernes, il est possible de mettre en oeuvre des algorithmes dynamiques de gestion des inventaires qui peuvent suggérer des points de réapprovisionnement et des quantités idéaux pour minimiser les coûts d'inventaire. Il s'agit d'un inventaire juste-à-temps pour une production juste-à-temps, sans excédent d'argent dormant dans les entrepôts !
Vous désirez en savoir plus?
Chez Différence, notre expertise est axée sur la statistique et la science des données, les applications du Lean et l'Excellence opérationnelle, ainsi que sur la simulation! N'hésitez pas à demander plus d'information en nous contactant.

