Optimisation robuste à l'aide des modèles d'apprentissage machine

Optimisation et apprentissage machine ensemble???

Les techniques modernes de la science des données ont ouvert de nouvelles façons d'optimiser les processus. Il est très tentant de rechercher des conditions hautement désirables directement à partir des données sans avoir à développer des simulations complexes. L'information existe déjà, dans le tableau de données, attendant juste d'être extraite... Pourquoi ne pas « simplement » développer des modèles d'apprentissage machine pour explorer et ajuster les données? Nous avons développé une approche permettant de créer automatiquement des modèles à partir des données, suivie d'une optimisation par boîte noire. En résumé, les étapes sont :

1. Normaliser les données et utiliser le clustering pour découvrir où les données se répartissent dans l'espace
2. Utiliser la modélisation prédictive pour capturer la relation entre les paramètres contrôlables/actionnables et les critères de performances (les forêts aléatoires sont utilisées par défaut)
3. Configurer une simulation Monte-Carlo : la variabilité autour de chaque candidat est évaluée pour estimer la robustesse ponctuelle (insensibilité aux perturbations locales)
4. Déclencher l'optimiseur : essayeritérativement de nouveaux candidats pour améliorer la valeur du critère de performance jusqu'à ce que l'optimiseur conclue à l'optimalité

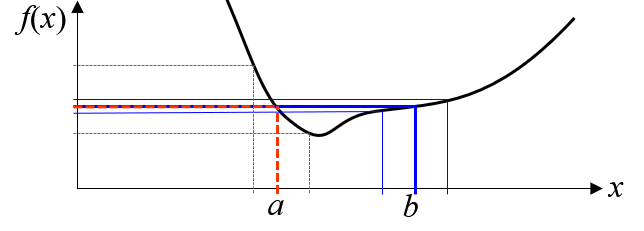
Un candidat est considéré comme « meilleur » que d'autres s'il est suffisamment proche des données historiques et si sa valeur prédite est inférieure ou supérieure (minimisation ou maximisation) au meilleur jusqu'à présent. Mais! Un compromis est accepté sur des points de robustesse exceptionnelle : de petites dégradations de performances en échange d'un gain de robustesse important. Ce compromis est illustré ci-dessous : les points a) et b) ont la même valeur, mais le point b) est plus intéressant car il réduit la variabilité de f(x).

Optimisation complexe se cherche des données!

Le problème d'optimisation qui en résulte est difficile car le gradient peut ne pas être défini, les données peuvent avoir des sous-groupes (domaine disjoint), la relation peut être non-linéaire et bruitée. La recherche et l'expérience conduisent à recommander l'algorithme MADS (mesh adaptive direct searches), un algorithme contemporain puissant (voir l'excellente description ici).

Cette approche d'optimisation basée sur les données nécessite... des données! Lorsqu’il y a au moins 20 observations par variable, cela donne des résultats très intéressants. Pour ajuster simultanément 10 paramètres, au moins 150 à 200 observations suffiront. Pour les ensembles de données plus volumineux, le clustering intégré et la modélisation prédictive géreront la taille afin que l'optimiseur reste ultra-rapide.

Un exemple utilisant des données de source libre

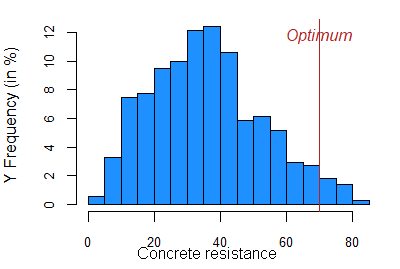
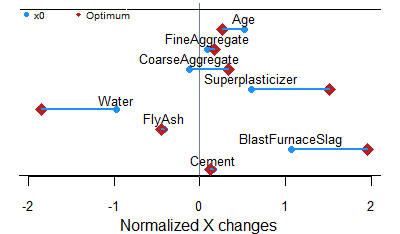
Nous avons réutilisé un ensemble de données de source libre sur des propriétés du béton. L’objectif est de déterminer la recette de mélange et les règles de préparation qui maximiseront de manière robuste la résistance du béton. Il s'agit d'un petit ensemble de données (1 030 observations, 9 variables), mais il est difficile pour les optimiseurs et très utile pour illustrer le comportement de notre approche robuste basée sur les données.

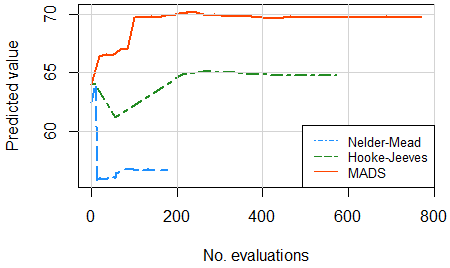
Cette première figure compare 3 algorithmes de recherche directe sans dérivées. En raison du compromis difficile entre performance et robustesse dans ce problème, seul MADS a réussi à augmenter la résistance du béton. La simulation Monte-Carlo sous-jacente a montré que la variabilité a été réduite d'un facteur 3!

Ces deux figures sont utiles pour voir où se situe l'optimum par rapport aux données et comment chaque variable a évolué entre le début et la fin de l'optimisation. L'optimum robuste n'est pas la valeur historique la plus élevée, mais c'est certainement la valeur robuste la plus élevée, comme le confirme la courbe de convergence MADS (ligne orange dans le graphique ci-dessus).

Adéquation parfaite entre optimisation et apprentissage machine!

Cette méthodologie, incluant l'algorithme MADS, a été implémenté dans R, un puissant langage de programmation mathématique. L'apprentissage machine est un moyen automatisé puissant de découvrir le domaine des données et de prédire les performances des processus. La simulation Monte-Carlo est un outil simple pour évaluer la robustesse ponctuelle aux perturbations locales. L'optimisation par boîte noire, plus précisément l'algorithme MADS, peut véritablement optimiser le problème résultant. Et il existe un optimum robuste obtenu directement à partir des données... La science des données peut être tellement passionnante!

Lire l'article complet ici.

Vous désirez en savoir plus?

Chez Différence, notre expertise est axée sur la statistique et la science des données, les applications du Lean et l'Excellence opérationnelle, ainsi que sur la simulation! Nous pouvons former, coacher et aider les praticiens à apprendre à utiliser l'optimisation. N'hésitez pas à demander plus d'information en nous contactant.